

Zusammenfassung.
Nicht Zählen, sondern Teilen wird in den Anfang der Mathematik gesetzt, womit eine Verbindung zwischen Mathematik, Musik und Sprache zum Vorschein kommt. Die Bezeichnung von Teilen des Ganzen und von Tonhöhenabständen durch 2k-Teile bringt ein auf Sinneseindrücken gestütztes spielerisches System hervor, mit dem sowohl mathematische Operationen und akustische Aussagen angezeigt werden können. Ausgehend von der Folge 3, 4, 7, 11, 18 … wurde die stetige Teilung, (1,618n…) = A, zur Erstellung einer Logarithmentafel mit ganzzähligen Logarithmen n und Numeri A, als Beispiel der bildhaften Dualarithmetik angewendet, womit Divisionen großer Zahlen leicht durchführbar sind. Die alten Tonsysteme abendländischer Musik werden mit mathematisch regelmäßigen Tonsystemen verglichen, und ihre Eignung zur Übertragung von Sinnesinhalten diskutiert.Es ist unwahrscheinlich, dass unser 'Erkennen' weiter reichen sollte als knapp zur Erhaltung des Lebens ausreicht. Die Morphologie zeigt uns, wie die Sinne und die Nerven, sowie das Gehirn sich entwickeln im Verhältnis zur Schwierigkeit der Ernährung" (Friedrich Nietzsche, "Der Wille zur Macht", 494).
4.1. Einführung. Viele Tiere singen. Der Mensch singt und spricht. Viele Tiere teilen. Der Mensch teilt und zählt. Ich vermute, dass bei Annahme einer Entwicklungsphase, in der man sowohl Begriffe wie mathematische Größen musikalisch ausdrückte, die geistige Entwicklung des Menschen kohärenter zu beschreiben wäre, da so das angeborene Streben nach Bündigkeit der Sätze der Bündigkeit der Natur entspricht.
Auch ich glaube, dass die Besonderheit dieser Spezies mit der Ernährungsart verbunden ist, doch nicht allein mit Nahrungsbeschaffung, sondern auch mit Nahrungsteilung. Nahrungsteilung löste Emotionen aus, förderte das Empfinden von Gerechtigkeit, stärkte zwischenmenschliche Beziehungen und beeinflusste Verstand. Es war eine der grundlagen emotionaler Intelligenz.4.2. Teilen fürs Leben. Zählen ist nicht überlebenswichtig. Tiere liefern den Beweis. Naturvölker lieferten ihn auch, doch wurden anderen belehrt. Bei Tieren ist es meist grobes Zerteilen, doch eine Vogelmutter, die alle Jungen durchbringen will, verteilt gleichmäßig. Eine kleine menschliche Gemeinschaft würde am ehesten ihre Mitglieder durchbringen, wenn sie das von ihnen zusammengetragene gleichmäßig teilte. Man kann es auf verschiedene Art tun. Mir kam dazu in den Sinn, dass in der Heimat meiner Jugend, wo Wege und Höfen oft nicht bepflastert waren, Kinder, auch kleine Kinder, Rechtecke in den Boden ritzten, um darauf zu spielen, doch ein Rechteck zu zeichnen für sie eigentlich zu schwierig sein sollte. Nun könnten gerade Kinder beim Verteilen von Nahrung sehr aufmerksam gewesen sein, da sie in der Regel weniger bekamen, und jedes unrichtige Teilen bemerkt und als ungerecht empfunden haben. Ein gerader Stock schräg über die Ecken eines Rechtecks gelegt teilt das darin Ausgebreitete offensichtlich in zwei gleiche Teile. Es könnten Nüsse, Beeren, Körner Muscheln und anderes gewesen sein, gelegt auf in Felsplatten geritzte Rechtecke vieles andere. Das Halbierte im Rechteck ausgebreitet wäre leicht auf ein Viertel zu halbieren, das wiederum auf ein Achtel. Damit wäre man allerdings auch schon am Ende, da ein Achtel der Menge meist zu klein ist, um es gleichmäßig im Rechteck auszubreiten.
Folgendes stellte sich heraus:
-Halbieren ist, unabhängig von der Größe des Teilers und der auf dem Teiler liegenden Menge, immer dieselbe Tätigkeit.
-Es besteht ein Zusammenhang zwischen der Zahl der Teilnehmer und dem auf den Teilnehmer zufallenden Teil, nicht jedoch mit der auf den Teilnehmer zufallenden Menge, die von Mahl zu Mahl verschieden war.
-Der Zusammenhang zwischen der Zahl der Teilnehmer und dem auf den Teilnehmer zufallenden Teil zeigt eine Verbindung zwischen 2 und 1/2, 3 und 1/3, 4 und 1/4, 8 und 1/8 usw.
Die Verdoppelung des Achtel zum Viertel, des Viertel zum Halben, des Halben zum Ganzen, ist der umgekehrte Vorgang. Ausgehend von einem Stein kann man mit Steinen auf denselben Rechtecken Verdoppelungen in umgekehrter Richtung spielen. Auch im Spiel der Verdoppelungen würde man allerdings nicht weit kommen, da schon nach vier Verdoppelungen und sechzehn Steinen im Spiel, das Spiel unübersichtlich und anstrengend würde. Man bemerkte jedoch, dass zum Spielen die wirkliche Anzahl der Steine eigentlich nicht nötig ist. Es genügte zu wissen, dass die Anzahl der Steine im nächsten Rechteck doppelt so groß, und im vorangehenden Rechteck halb so groß ist, und vereinbaren, dass in Richtung links die Steinmengen wachsen, in Richtung rechts sich verringern. Zur besseren Übersicht wäre nach allen vier Rechtecken eine doppelte oder stärkere Linie in den Boden zu ritzen. Ein Stein im äußeren rechten Rechteck ist jetzt tatsächlich ein Stein, ein Stein in den links nächsten Rechtecken zeigt 2, 4, 8 usw. Steine an. Das Fehlen eines Steines im Rechteck zeigt "keine Steine".
Fürs Weitere wird das Wort "Rechteck" durch das kürzere "Feld".
Aus der Grundregel des Spiels folgt, dass zwei Steine auf einem Feld durch einen Stein auf dem nächst linken Feld ersetzt werden können.
Unter den vielen Anordnungen des Spiels ist folgende von besonderen Interesse:
Mit einem zusätzlichen Stein im äußeren rechten Feld:

Wäre es die Anordnung:
Die anfängliche Anordnung mit vier Steinen wäre bei Annahme, dass ein schwarzer und ein roter Stein auf demselben Feld aus dem Spiel ausscheiden, also leeres Feld bedeuten, durch folgende zu ersetzen:
Die arithmetische Beschreibung des Vorganges wäre:
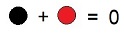
womit die arithmetischen Operationen Addition und Subtraktion zu spielen wären.
Beispiele.
Addition
116+98=214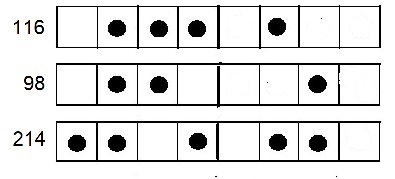
Subtraktion 214-98=116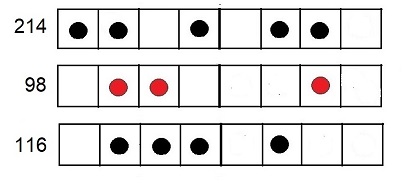
Multiplikation ist auf Halma- oder Schachbretten entsprechender Größe auch mit großen Zahlen, wie im Beitrag "1.2 Magisches Denken und die Logik der alten mathematischen Systeme", Absatz 2.8, gezeigt, leicht zu spielen. Hier nur ein kurzes Spiel auf einer 4x5 Feld Tafel, das den spielerischen Vorteil des Einsatzes roter Steine zeigt.
9x15=135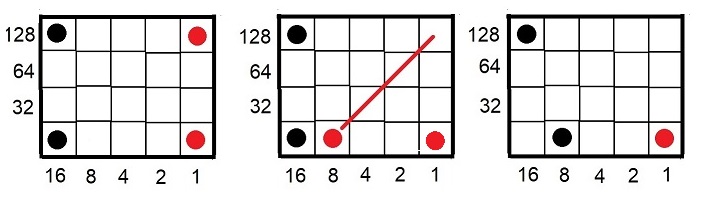
Teilen dagegen ist im Spiel langwierig. Am leichtesten Teilen von 1, wie im Beitrag 1.2 gezeigt. Divisionen werden dann anhand einer Tafel von Kehrwerten als Multiplikation durchgeführt.
Ansonsten sind die für Stellenwertsysteme üblichen Verfahren anzuwenden, da das Spiel dem Dualsystem mit der zusätzlichen Zahl -1 entspricht, wobei Rot Schwarz auf Rot, und Rot auf Schwarz verfärbt.
Das Spiel ist leicht auf Halbierungen des Ganzen auszudehnen. Bezeichnet man die Mitte einer Reihe von Quadraten ein Quadrat als "Eins", dann sind darauf zugleich Verdoppelungen von "Eins" und Halbierung von "Eins" darstellbar. Das Quadrat für 1 ist stärker eingezeichnet. Für 13+13/16 wäre zum Beispiel:
4.3. Die stetige Teilung. Die Proportionen der stetigen Teilung findet man in Architektur und bildender Kunst der Antike und des Mittelalters. Beschrieben wurde sie erstmals von Euklid, doch war früher bekannt. Im 13. Jahrhundert beschrieb Fibonacci die nach ihm genannte Zahlenfolge, mit der man auf diese Proportion kommt. In der Renaissance suchte man sie in der Natur. Aus dieser Zeit stammt der Name "Divina Proportio". Seit dem 19 Jh. bezeichnet man sie als "Goldener Schnitt".
Rätselhaft ist das Pentagramm, ein Zeichen, dessen Abschnitte im Verhältnis des Goldenen Schnitts stehen. Es ist uralt. Schon um 3000 v.Chr. war es das Symbol der sumerischen Göttin Inanna. Auch in späteren Kulturen wurde es verehrt und ist bedeutsam bis heute. Wie kam es, dass diese so komplizierte geometrische Figur so früh zum Symbol wurde?
Der Besonderheit des Dualsystems liegt eine mathematische Unregelmäßigkeit zugrunde. Es ist nämlich: 2+2=2x2. Es gilt auch für die Beziehung: hn+hn+1 = hn+2, für h = 1,618…, worin "h" die "Goldene Zahl", "n" eine reelle Zahl. Beispiel: 1,6181,1416 + 1,6182,1416 = 1,6183,1416
Für n = -1 ist h = 0,618…, womit der Abstand zwischen der Zahl und ihrem Kehrwert gleich 1 ist.
Die Fibonacci Zahlen werden entsprechend der Rekursionsformel: an = an-1 + an-2 gebildet, woraus sich die Glieder der Folge 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 usw. ergeben. Schon für 144/89 ist 1,617977.Es gibt eine andere Folge, nämlich 3, 4, 7, 11, 18, 29, 47, 76, 123, usw., die dieselbe Eigenschaft hat (123/76 = 1,618421), deren Glieder sich zudem schnell den nahezu ganzzahligen Potenzen von 1,618. nähern, z.B. 1,61810 = 122,992. Daraus ergibt sich die Möglichkeit des Ersetzens von Division durch Subtraktion und Multiplikation durch Addition. Dazu eine Zusammenstellung der Potenzen von 1 bis 16 und ihrer Kehrwerte. Die Zahl 1,618. wird mit h bezeichnet. Zur Berechnung wurde 1,618034 genommen.
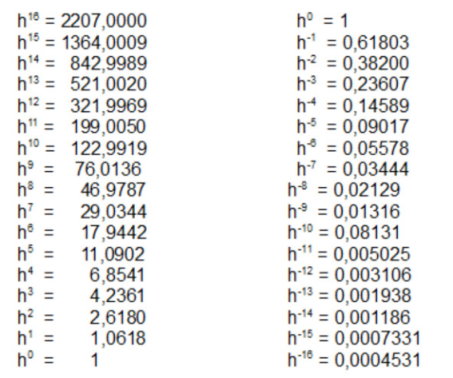
Die Zahlen werden in die Reihenfolge der Logarithmentafeln gestellt.

Mit dieser Tafel kann man zwar Divisionen und Multiplikationen bis zur dritten Dezimalstelle genau ausführen, z.B.
3,220:6,180 = h12×10-2:h-1×101 = h13×10-3 = 521×10-3 = 0,521, doch sie ist praktisch unbrauchbar, da die Abstände zwischen den Zahlen zu groß sind.Dasselbe in der Arithmetik des Spieles. (Die Kreise vor den Steinen wurden aus darstellungstechnischen Gründen gesetzt.)

Die Annäherung für h 16≈ 2207 ist ausreichend genau, da h 16 = 2206,9998. Zur Bestimmung der niedrigen Potenzen von h wird h 17 durch h18 geteilt (3571/5778 = 0,6180339), was leicht zu spielen ist, da die leeren Quadrate des Minuenden mit dem nächst linken Stein aufgefüllt werden, aber auf dem Blatt nicht gezeigt werden kann, und wie hier durchgeführt schwierig nachvollziehen ist. Die erste Zeile ist der Quotient. Hinter dem markierten Kreis beginnen Halbierungen (1/2, 1/4, 1/8, …).
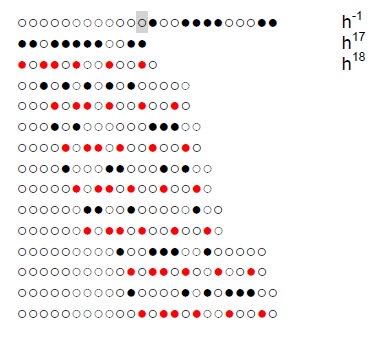
Der Quotient ist mit 0,617996 bis auf 1/10000 genau. Mit 1 addiert ergibt h1, h1 mit 1 addiert ergibt h2, und so weiter, wie folgt:

Ab h10 sind im Spiel mit 12 Quadraten die Werte der mit den Zahlen 3 und 4 beginnenden Folge genauer.
Zur Bestimmung der Kehrwerte wäre 0,618 von 1 zu subtrahieren, die Differenz von 0,618, usw.

Man kann jedoch die Kehrwerte auch durch Addition ermitteln, was leichter zu zeigen ist als Subtraktion. Dazu wurden die Kehrwerte von h-16 und h-15 bestimmt (hier nicht gezeigt).

In den Bereich von 1 bis 2 des Dualsystems gestellt, verkleinert sich der Abstand der Zahlen, wodurch die Tafel brauchbar wird. Die runden Steine der Zahlen und die quadratischen Steine der Exponenten sind in der den Logarithmentafeln entsprechenden Reihenfolge eingezeichnet. In der linken Spalte sind die den dezimalen Zahlen entsprechenden dualen Zahlen von 1 bis 2 in Form schwarzer Kreise als Summe von 1 (schattiert) und Halbierungen von 1 angeben. Der Abstand zwischen den Zahlen würde sich durch heranziehen weiterer Potenzen von 1,618… entsprechend verkleinern. In der rechten Spalte stehen blaue Quadrate für positive ganzzahlige Exponenten über 1,618… und gelbe Quadrate für negative ganzzahlige Exponenten über 1,618… Daneben positive (schwarz) und negative (rot) ganzzahligen Exponenten über 2. Das "x" dazwischen bedeutet Multiplikation. Es sind die Mantissen. Leere Kreise und Quadrate bedeuten nicht belegte Felder.

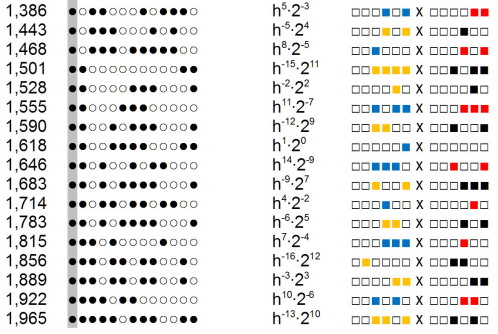
Zur Ausführung von Multiplikationen werden die Quadrate aufeinander gelegt. Zwei Quadrate derselben Farbe auf demselben Feld (derselben Stelle) sind durch ein Quadrat auf dem nächsten linken Feld zu ersetzen. Zwei Quadrate unterschiedlicher Farben auf demselben Feld werden vom Feld genommen. Bei Divisionen werden die Quadrate des Divisors mit verkehrten Farben aufeinandergelegt.
Beispiel.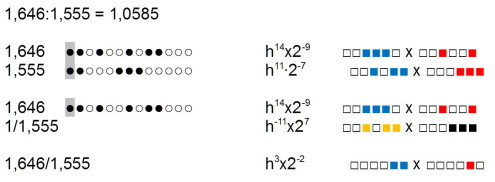
Zur Bestimmung der Kehrwerte werden die Vorzeichen der Exponentenumgekehrt.
Zum Beispiel:
3/2 ≈ h-15×211; 2/3 ≈ h15×2-11 = 0,6660;
19/16 ≈ h9×2-6; 16/19 ≈ h-9×26 = 0,8420; 1/19 ≈ h-9×2 2 = 0,05262; 1/19 = 0,05263;Eine Tafel mit Potenzen von -256 bis +256 gäbe einen Abstand der Zahlen in linken Spalte der Tafel von etwa 1/1000. Diese Tafel, sowie diedazu gehörende Tafel mit Potenzen von -512 bis +512, sind im Spiel in 12 Quadraten schnell und mühelos auszufertigen. Die Beschleunigung von Divisionen und Multiplikationen wäre für die primitive Mathematik ein Durchbruch, wie ihn Logarithmen herbeiführten. Und könnte erklären, warum man dessen in Symbolik und Architektur gedachte.
Wie würde sich stetige Teilung anhören? Vorstellbar ist ein Saiteninstrument mit Saiten gestimmt auf 29, 47, 76, 123, 199, 322, 521, 843, 1364, 2207, 3571, 5778, 9349 und 15127 Hz und den entsprechenden Duallogarithmen 4,858; 5,555; 6,248; 6,943; 7,637; 8,331; 9,025; 9,719; 10,414; 11,108; 11,802; 12,496; 13,191; 13,885. Die Differenz zwischen 4,858 und 5,555 beträgt 0,697. Ab 7,637 ist es abgerundet 0,694. Für die Fibonaci Zahlen 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711 sind es die Duallogarithmen 5,087, 5,781, 6,476, 7170, 7864, 8,558, 9,253, 9,947, 10,641, 11,335, 12,030, 12,744, 13,418, 14,112. Die abgerundete Differenz beträgt ebenso 0,694. Mit Saiten unterschiedlicher Farbe wären beide Tonsysteme spielbar auf einer 28-Saiten Harfe.
4.3. Teilen im Gehör. Das menschliche Ohr empfindet gleichmäßige Luftdruckstöße bei Frequenzen von über 16 Hz als Töne. Der Hörbereich liegt zwischen 16 und 20000 Hz, doch sinkt im fortgeschrittenen Alter bis auf 5000 Hz. In der Musik wird der Hörbereich in Oktaven aufgeteilt, mit dem obersten Ton der doppelten Frequenz des untersten. Für die Oktave, die mit dem eingestrichenen "c" beginnt, ist es heute 261,626 Hz, um 1900 war es meist 259 Hz, in der altenglischen Stimmung etwa = 256 Hz, in der physikalischen Stimmung exakt 28= 256 Hz. Töne, deren Schwingungszahlverhältnis sich um 2 unterscheidet, werden als höhere bzw. tiefere Wiederholungen desselben Tones empfunden. Es ist eine angeborene Eigenschaft, die als Oktavverwandtschaft bezeichnet wird. Das Unterscheidungsvermögen der Tonhöhen ist beim Menschen gut ausgebildet. Die Unterscheidungsschwelle liegt bei 0,3% (1/300 des Oktavabstandes) im Bereich zwischen 1000 Hz und 3000 Hz. Es sind allerdings individuelle Leistungen des Gehörs, die sehr verschieden sein können.
Das besondere am Tonhöhenempfinden ist, dass es nicht den Frequenzen, sondern dem Logarithmus dualis (ld) der Frequenzen entspricht. An Trommelfell und Schädelknochen stoßen Schallwellenbestimmter Frequenz, im Gehirn nehmen wir Logarithmen dieser Frequenzen wahr. Mit f für Frequenz und k für Tonhöhe wären es am Eingang des Systems Numeri bzw. Potenzen,im System aber Logarithmen bzw. Exponenten, gemäß k=ldf bzw. f=2k. Wir können Frequenzen quantitativ festlegen, indem wir sie messen. Es ist physikalische Realität. Wir können Töne quantitativ schätzen, weil wir deren Höhe empfinden. Es ist geistige Realität. Da durch Rechnen mit Exponenten die Rechenarten um eine Stufe herabgesetzt werden, könnte man die den Frequenzen von 24, 25, 26,...entsprechenden Tonhöhen mit den Zahlen 4, 5, 6,… assoziieren, ebenso Bruchteile der Exponenten.
Die Frequenz des tiefsten hörbaren Tons beträgt 16 Schwingungen in der Sekunde oder dem 1/86400 Teil des mittleren Sonnentages. Die Zahl 24 Hz/Sekunde ist ein wundersamer Zufall, über den nachzudenken wäre, da er an die unverständlichen mathematischen Regelmäßigkeiten der Zeitrechnungen der Maya erinnert. Mit einer anderen Zeiteinheit, z.B. mit dem 1/100000 Teil des Tages, wie sie während der Französischen Revolution festgelegt wurde, ergäbe sich für den tiefsten hörbaren Ton nicht 16 Hz. Die Möglichkeit, dass unsere Zeiteinheiten auf die Zahl 16 ausgelegt wurden ist unwahrscheinlich, doch mit 16 Hz und 2k-Vielfachen von 16 Hz werden die Ausführungen leichter.
Im Weiteren werden die Musiksysteme der abendländischen Musik, nämlich das harmonisch-reine (in seiner C-Dur Tonart), das pythagoreische und das gegenwärtige 12-stufige gleichmäßige System, mit dem 16-stufigen gleichmäßigen System, (es schließt das 4- und 8-stufige System ein), zur Herausstellung der Unterschiede auf die dem Spiel entsprechende Art mathematisch verglichen. Zur Verdeutlichung wird zudem das erwähnte Farbspiel eingesetzt, in dem Halbierungen und Verdoppelungen mit Farben dargestellt sind, z.B. mit farbigen Steinen oder Karten. Es wird entgegen dem bisherigen "Langen Spiel", "Kurzes Spiel" genannt, da es auf engsten Raum, ohne Feldbrett und Einhaltung der Steinordnung gespielt wird. Für das folgende Spiel wurden Farben in der Reihenfolge des Regenbogens gewählt. Sie bezeichnen die durch Halbierungen des Oktavabstandes hörbaren Abstände 1/2, 1/4, 1/8,… Mit 8 Farben (für 1/2 bis 1/256) ist die Tonhöhenunterscheidungsschwelle erreicht.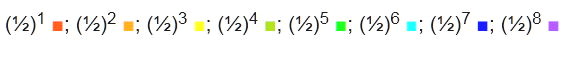
In der rechten Spalten sind die Duallogarithmen von Frequenzverhältnissen zweier Töne angegeben. Duallogarithmen, da ich mich auf eine Vergangenheit beziehe, in der Frequenzen und Saitenlängen noch nicht gemessen wurden. Das Lange Spiel (die äußerste rechte Spalte) wird bis 2-16 geführt.

Die Frequenzverhältnisse des gleichmäßigen 12ton Systems und des gleichmäßigen 16ton Systems klingen wohl, obwohl sie meist von den Frequenzverhältnissen der harmonisch-reinen Stimmung stark abweichen - und sie schließen die "Harmonielücke" zwischen Quarte und Quinte. Ich vermute, dass nach Entwicklung des Empfindens der Oktavverwandtschaft, als erstes die Tonhöhe der halbierten Oktave deutlich hörbar war, danach die Tonhöhen der geviertelten Oktave. Es wäre die Grundlage eines einfachen, dem Musizieren auf Instrumenten vorangehenden, gleichmäßigen 4ton Gesangsystems. Mit nur vier Tonhöhen der geviertelten Oktave wären die Töne leicht unterscheidbar, folglich könnte derartiges System schon früh ausreicheichend verständliches Sprechen ermöglicht haben. In einer Entwicklungsphase als der Stimmapparat noch raue, unscharf abgegrenzte Laute hervorbrachte, aber Sprecher die Oktavverwandtschaft und Tonhöhenunterschiede schon empfanden, könnte die Entwicklung von Tonsprachen d.i. Sprachen, in denen die Bedeutung des Wortes durch die Tonhöhe des Vokals bestimmt wird, eine Notwendigkeit gewesen sein. Die meisten Sprachen sind auch gegenwärtig tonal. Die indogermanischen Sprachen sind es nicht, doch Litauisch, Lettisch, die skandinavischen und einige Sprachen des Balkans weisen Merkmale der Tonsprachen auf. Ebenso einige Mundarten, wie das Ripuarische in Deutschland. In der Linguistik werden nicht tonale Sprachen als Ausgangssprachen angenommen, von denen Tonsprachen in Folge von Konsonantenerosion abstammen. Es könnte umgekehrt gewesen sein. Vor 1200 Jahren unterschied das Chinesische acht Tonhöhen, heute sind es fünf. Altgriechisch war eine Tonsprache, Neugriechisch ist es nicht mehr. Innerhalb der meisten Tonsprachen vollzieht sich eine Abflachung der Tonhöhen. Die Ausgangsformen mit gleichbleibenden Tonhöhen gehen in Formen mit steigenden und fallenden Tonhöhen und schließlich in Tonakzentsprachen über. Der leichter realisierbare Druckakzent setzt sich durch.
Als Beispiel eine denkbar einfache Tonsprache mit Worten aus 3 von 4 Tönen der geviertelten Oktave, bestehend aus 64 fonetisch notierten Wörtern. Allerdings müssen Wörter einer Sprache, die mit 64 Wörtern alles sagen möchte, sehr allgemein sein, die Sätze sind dann zwangsläufig vieldeutig. Es kann nur eine Orakelsprache sein, wie das ebenfalls aus 64 Begriffen, den Hexagrammen, bestehende I-Ging , seine Zeichen jedoch erklärt werden müssen. Wohlgemerkt, das I-Ging ist ein zur höchsten Abstraktion gebrachtes System, von formeller Schönheit nicht zu überbieten, doch es ist "stumm".
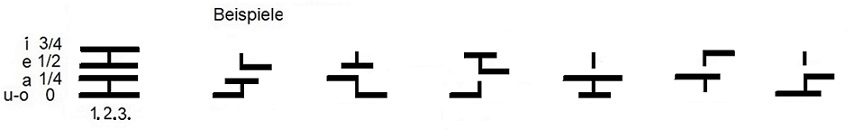
Die vertikal angeordneten Zahlen zeigen die Aufteilung der Oktave an. Die horizontalen Zahlen – die Reihenfolge der Töne. "0" ist der Grundton. Die Vokale selbst, sowie ihre Stärke und Länge sind bedeutungslos. Ebenso Konsonanten, falls eingesetzt zur Erleichterung der Aussprache. Der vertikale Strich zeigt lediglich die Positionierung der horizontalen Striche an.
Mit zwei Zeichen für ein Wort wäre es mit 642 = 4096 Worten in einer statischen Kultur wie das altertümliche China eine langsame, aber brauchbare Sprache. Langsam, da man zum Benennen des Besonderen zwei von den 64 allgemeinen Worten zusammenstellen müsste, was eine dafür zuständige geistige Instanz voraussetzt, wie es, im Alten China gewesen zu sein scheint. Das I-Ging zeigt nämlich Sprache als Wissenschaft der Begriffsbildung und Schule des Denkens. Ein Begriff für magnetische Erscheinungen vorgegeben durch die drei allgemeinen Begriffe "Kraft", "Fernwirkung" und "Drehung" wäre jedenfalls sinnvoller als die Benennung mit dem Namen einer Gegend im antiken Griechenland. Dann würde man auch bemerken, dass Begriffe wie "Quantenchromodynamik" nur verschwommene Phrasen sind. Sprache, in der man sofort weiß, führt leicht in Illusion.
Die tonalen Sprachsysteme zerbrachen in den aufkommenden dynamischen Zivilisationen mit schnell wachsender Anzahl von Gegenständen und veränderlichen gesellschaftlichen Verhältnissen. Für die neuen Worte wurden Konsonanten als Träger von Bedeutung hinzugezogen, was mit der Zeit zur tonalen Verflachung und dynamischen Wortakzent (Tonstärke) führte. Es war eine epochale Veränderung erwähnt im Alten Testament, als Verwirrung der Sprache (1.Mose11,7).
Demetrios, ein alexandrinischer Philosoph des 2. Jh., berichtet in seiner Schrift "Über den Stil" folgendes: "In Ägypten singen die Priester Hymnen an die Götter, in dem sie die sieben Vokale hintereinander aussprechen. Deren Klang macht auf die Zuhörer einen tiefen musikalischen Eindruck, wie wenn Flöte und Leier verwendet würden… aber vielleicht ist es besser, wenn ich nicht mehr über dieses Thema spreche". Warum? Der musikalische Eindruck entstand vermutlich dadurch, dass die Vokale in unterschiedlichen Tonhöhen ausgesprochen wurden. Gedachte man einer uralten Sprache?
Ich glaube nicht, dass dem Menschen die Fähigkeit des Denkens geschenkt wurde. Ebenso wenig, dass das Genie eines Johann Sebastian Bach von gelegentlich musizierenden Sammlern und Jägern herkommt.
Fassung: Juni 2023