I.2. MAGISCHES DENKEN UND DIE LOGIK DER ALTEN MATHEMATISCHEN SYSTEME
                 Binäre Ordnung in den Verfahren der Sumerer, Alten Ägypter und Maya

Zusammenfassung. Die altertümlichen Zahlensysteme mit hoher Basis, wie das sexagesimale Zahlensystem (2⁶-4) der Sumerer und die als magisch geltende Periode der Chronologie der Maya von 260 (2⁸+4) Tagen, werden als Überganssysteme zur Umrechnung von Dezimal- bzw. Vigesimalzahlen in ein 2^k-Zahlensystem und umgekehrt erklärt. Zahlen werden durch eine Summe von Stufenzahlen, die ihre besonderen Zeichen haben, dargestellt, doch können direkt in Zahlen eines 2^k-Stellenwertsystem verwandelt werden. Die Bruchrechnung der Ägypter wird auf unendliche Dualbrüche, die im dezimalen System stets als endliche Summen unterschiedlicher Stammbrüche darstellbar sind, zurückgeführt. Die Hypothese wird des Weiteren mit altertümlichen Rechenverfahren, Systemen von Maßeinheiten, linguistischen Indizien, Symbolen und Spielen begründet.

      2.1. Die Anfänge mathematischen Denkens, obwohl gut bekannt und viel diskutiert, bleiben unverständlich. Die Verfahren sind umständlich, entwickelten sich im Laufe von Jahrtausenden wenig, in einigen Bereichen ist ein deutlicher Rückgang feststellbar. Lehrsätze gibt es nicht, Beweise wurden nicht durchgeführt, Gleichungen nicht formuliert. Andererseits finden wir gleich am Anfang Kenntnisse, die erst nach Jahrtausenden von den Griechen oder später wiedergewonnen wurden, wie die pythagoreischen Zahlentripel bis (13500, 12709, 18541) oder der bis auf die fünfte Dezimalstelle genau errechnete Wert der Qua­dratwurzel aus 2. Zu den großen Rätseln dieses Anfanges gehört das sexagesimale (60er) Zahlensystem der Sumerer, ein um Jahrtausende vor den Indern entwickeltes Stellenwertsystem, dem nur die Null fehlte. Die hohe Zählbasis bleibt unerklärt. Eine Weiterentwicklung der Kunst des Zählens an Fingern von Händen und Füßen ist es nicht. Die Ableitungen vom altertümlichen Jahr von 360 Tagen, von der Aufteilung des Kreises mit dem Radius, der guten Teilbarkeit der Zahl 60 oder der Notwendigkeit einer gemeinsamen Vielheit zweier Gewichtseinheiten, der sumerischen Mine und des akkadischen Schekel überzeugen nicht. Die sumerischen Zahlwörter entstammen zum Teil dem Fünfersystem (6=5+1, 7=5+2), zum Teil dem Zehner- bzw. Zwanzigersystem (30=20+10, 40=20×2, 50=20×2+10); die Zahlennotation beruht auf Wiederholungen der Zahlen 1 und 10. Für praktische Berechnungen wurde parallel das Zehnersystem genutzt. Es war ver­mutlich das ursprüngliche Zahlensystem. Warum rechneten dann Mathematiker und Astronomen im Sechzigersystem? Die gute Teilbarkeit der Zahl 60 ist kein Ausgleich für eine Multiplikationstafel, die man stets bei Hand haben muss, da das kleine Einmaleins mit 3600 endet. Sprachliche Nachteile kommen hinzu. Man erklärt die Verdrängung des Fünfersystems und des Zwanzigersystem durch das Zehnersystem mit der Unbequemlichkeit von zu kurzen bzw. zu langen Reihen von Zahlwörtern der Zählbasis, was umso mehr für das Sechzigersystem gelten sollte. Sein Verschwinden ist demnach erklärbar, sein Erscheinen nicht.

Es war keine sonderliche lokale Erfindung. Dem alten chinesischen Kalender mit fortlaufend nebeneinander gesetzten Namen von zehn himmlischen Stämmen und zwölf irdischen Zweigen liegt der 60er Zyklus zugrunde. Die Inder hatten eine 60er Teilung des Tages. In Europa rechnete man in einem Zwölfer-Zehner Zahlensystem, mit Schock (60) und Großhundert (120). Alte Kalender umfassten lediglich eine Periode von 360 Tagen, obwohl ihre praktische Unbrauchbarkeit schnell an den Tag kam, besonders in Ägypten, wo die regelmäßige Nilschwelle schon nach zehn Jahren um 52 Tage zurücklag. Dennoch hielt man daran Jahrtausende lang fest. Dem ägyptischen Mythos zufolge wurden die fünf fehlenden Tage gegen den Willen des obersten Gottes Re dem Kalender zugefügt.

      2.2. Die Maya hatten ein voll entwickeltes zwanziger Stellenwertsystem mit Null, versag­ten sich jedoch im "Long Count", (mit dem sie die Anzahl der Tage von einem Fixpunkt im 4 Jt. v. Chr. rechneten) aller Vorteile des Zwanzigersystems und rechneten anstelle der Stufenzahlen 400, 8000, 160000, usw., mit Einheiten von 360 (Tun), 7200 (Katun), 144000 (Baktun), usw., Tagen. Neben dem Tun (T) von 360 Tagen, als Zählbasis des Long Counts, rechneten sie in Zyklen von 365 Tagen (H, Sonnenjahr, "Haab"), von 260 Tagen (Z, Heiliges Jahr, "Tzolkin"), aufgeteilt in 20 Perioden zu 13 Tagen, außerdem im Zyklus von 584 Tagen (V, "Synodische Umlaufzeit des Pla­neten Venus") und in Zyklen von 7 Tagen und 9 Nächten. Alle 52 Sonnenjahre (R, "Kalenderrunde") liefen Haab und Heiliges Jahr zu R=52H=73Z zusammen, jede zweite Kalenderrunde (deren Ende mit größerem zeremoniellen und architektonischen Aufwand gedacht wurde) waren es drei Zyklen 2R=104H=146Z=65V. Mit R=52T+Z schlossen sie den Tun der Kalenderrunde an. Schalttage nutzten die Maya nicht, da es den Lauf der Zeit stören würde, doch aufgrund ständiger astronomischer Beobachtungen wussten sie stets um wie viele Tage die Sonne zurücklag, bzw. der Planet Venus voraneilte (die synodische Umlaufszeit der Venus beträgt 583,92 Tage).

Das mit verzahnten Rädern eines Uhrwerkes vergleichbare System ist eine geistige Leistung ohnegleichen, allerdings eine Leistung der Arithmetik, da bei aller Präzision, die Zyklen der Maya am Sonnenzyklus vorbeiliefen, und die für Landwirtschaft und Astronomie nötigen Daten ständig errechnet werden mussten. Rätselhaft vor allem ist das Heilige Jahr, das getrennt von den natürlichen Zyklen seine Touren dreht, und - wie man vermutet - nur dem religiösen Leben und der Wahrsagerei diente. Dafür also der enorme mathematische Aufwand? Man erklärt es mit magischem Denken. So etwa U. Schlenther⁶: "Die sich immer wieder folgenden Zwanzig ergaben aber noch keine größere fest zu fixierende Einheit. Aus diesem Grunde wurden im mesoamerikanischen Kulturbereich die Zahlen 1-13 hinzugefügt... In der 13 haben wir wahrscheinlich eine alte kultische Zahl zu sehen, vielleicht symbolisiert sie die dreizehn Monate des alten Mondjahres . So kam es aber auch, dass man die verschiedenen Zeiten des Jahres mit magischen Kräften in Verbindung brachte. In erster Linie waren es der Bedeutung nach Regen- und Feuchtigkeitsdämonen und die Winddämonen. In den zauberisch-animistischen Zeiteinteilungen galten besondere Zeiteinteilungen als gut oder schlecht, und zwar nicht nur allgemein, sondern sie waren noch speziell unterteilt in Bezug auf Aussaat, Feldarbeiten, Ernte, usw. Die Zeitabschnitte liegen innerhalb der 260d des magisch rituellen Kalenders. Er hat sich so primitiv er war, bis heute erhalten. Er diente und dient ausschließlich als Wahrsagekalender." Doch das Heilige Jahr wurde auch in rein mathematische und astronomische Beziehungen eingesetzt. Der Codex Dresdensis gibt mit 3mal 260 eine gute Annäherung der synodischen Umlaufszeit des Planeten Mars von 779,936 Tagen. Im Codex Peresianus sind 7 Heilige Jahre mit 5 Perioden von 364 Tagen (7·260=5·364) zusammengestellt, was mit 28-Tage Perioden und 13 Tageszeichen auf ein 364-Tage Jahr und auf die Einbeziehung der Periode von 7 Tagen weist (52·7=364). Des Weiteren wurden 405 Mondumläufe 11960 Tagen gleichgesetzt, was ungemein genau ist (der exakte Wert beträgt 11959,893 Tage), und interessant dadurch, dass 405 Mondumläufe mit 46 Heiligen Jahren zusammenfallen (46·260 =11960). Auch der Metonische Zyklus von 19 Jahren gleich 235 Mondumläufen oder 6940 Tagen ist mit Heranziehung des Heiligen Jahres ausgedrückt: es ist nämlich ein Katun vermindert um ein Heiliges Jahr (7200-260=6940). Man möchte fast glauben, dass die Zahl 260 eine unbekannte Naturgesetzlichkeit in sich birgt, die mit genügend Scharfsinn ergründbar wäre. Und wenn man noch zur Kenntnis nehmen muss, dass 29 Kalenderrunden oder 1508 Sonnenjahre genau 1507 tropischen Jahren T gleichen, da 29·52·365/1507 = 365,242203, dann wird einem schwindelig. Sie verstanden was von Astronomie, die Maya. Von Zeitrechnung übrigens auch. Einiges wäre fortschrittlich auch in unserer Zeit. Der auf den Tag genau festgelegte zeitrechnerischere Festpunkt. Bezeichnung des ersten Tages als Nulltag. Zeitrechnung durch Aufzählung von Tagen. Dieselbe Reihenfolge der Tagesnamen in allen Monaten desselben Jahres. Ein Kalender, der das Geburtsdatum innerhalb der Kalenderrunde eindeutig anzeigt, aber das Alter nicht zu erkennen gibt. Der Begriff der "namenlosen Tage" für die fünf letzten Tage des Kalenderjahres. Datierung, die Vierjahresperioden anzeigt, die sich für eine Korrektur des Kalenderjahres vorzüglich eignen. Korrekturtafeln zur Kalenderrunde, aus denen sich ein Jahr von 365,2420 Tagen errechnet. Anderseits, wüssten sie mit welcher Genauigkeit ihr System das tropische Jahr anzeigt, sollten sie sich die mühseligen astronomischen Beobachtungen und Berechnungen, ebenso das Steinhauen von Glyphen und anderes, das sie so berühmt macht, erspart haben. So klug und so dumm, diese Steinzeitmenschen? In der Tat, nach den allgemein anerkannten Kriterien stehen sie kulturell niedriger als die Bantu Völker Afrikas vor der Ankunft der Europäer, denn diese nutzten, wie die Maya, den Grabstock in der Landwirtschaft, doch betrieben zudem Viehzucht und schmolzen Eisen und Kupfer.

      2.3. Die größte Eigentümlichkeit ägyptischer Arithmetik ist die Bruchrechnung. Außer von 2/3 stellten sie Brüche als Summe von Stammbrüchen dar und führten Operationen mit Brüchen erst nach ihrer Zerlegung in Stammbrüche durch. Dazu nutzten sie Tabellen, in denen Brüche der Form 2/n (für ungerade n ) als Summe von Stammbrüchen aufgeführt sind. So war z.B. 2/5=1/3+1/15, 2/7=1/4+1/28, und ausschließlich diese Formen wurden in die Berechnungen herangezogen. Es durfte also nicht die banale Form 2/5=1/5+1/5 sein, aber auch nicht 2/5=1/4+1/12+1/15 oder eine andere. Dabei haben sie den Stammbruch als Zahl für sich aufgefasst, da sie ihn von der ganzen Zahl nur durch ein Zeichen über der Zahl unterschieden. Ein Zeichen für Addieren der Stammbrüche gab es nicht. Das Ergebnis einer im Papyrus Rhind enthaltenen Aufgabe, die man etwa mit: "Haufen; 2/3 und 1/3 und 1/7 des Haufens und der Haufen selbst ergeben 33. Wie groß ist der Haufen?" übersetzen könn­te, sieht dann auf ägyptisch so aus:

14+1/4+1/56+1/97+1/194+1/388+1/679+1/776 für die gemischte Zahl 14 28/97 (14+28/97).

Viel dümmer geht es nicht mehr. Zu dumm, dass man es mit Magie erklären könnte.

      2.4. Mit der Einführung des Internationalen Einheitensystems wurden dezima­le Vielfache und dezimale Teile von Einheiten gesetzlich festgelegt und die Übereinstimmung des Maßsystems mit dem Zahlensystem hergestellt. Nicht ganz, denn Stunde und Minute werden weiterhin rechtmäßig auf 60 geteilt, der Vollwinkel auf 360, und in rückständigen Gebieten weiterhin Pints getrunken und Gallonen getankt. Maßeinheiten haben, wie es scheint, ein zähes Leben. Ein Überblick über die Gesamtheit der Maßeinheiten, die bis zur Französischen Revolution im Gebrauch waren, zeigt, dass die mit dem Zehner­system übereinstimmenden Maßeinheiten in Minderheit sind. Es waren, z.B., das ägyptische Gewichtsmaß 1 neben = 10 kite, das griechische Längenmaß 1 plethron = 100 Fuß, die römische Meile geteilt in 1000 passus. Die Mehrheit dagegen bildet reine binäre Folgen, 2^k×10ⁿ-Folgen, entspricht dem Sechzigersystem, wie das babylonische Raummaß 1 pi = 60 sila oder dem Zwölfersystem, wie das preußische Längenmaß 1 Rute = 2 Klafter = 12 Fuß = 72 Zoll = 144 Linien. Die binären Einheiten gehören zu den ältesten. Ein vorgeschichtliches Gewichtssystem der Induskultur (Mochendscho-Daro, Harappa)⁵ nutzte folgende Vielfache von 0,8565 Gramm: 2, 4, 8, 16, 32, 64, 80, 200, 320, 640, 1600, 3200, 6400, 8000 und 12800. Die Alten Ägypter teilten den Fuß in 16 Fingerbreiten, den Klafter in 4 Ellen, den großen Schoinos in 2 Parasangen, den Parasange in 4 Meilen, den Char (Sack) in 4 Hehat. Am Fuße der Statue des sumerischen Fürsten Gudea von Lagesch (3 Jt.) sind 16 gleiche Teile eingezeichnet. Ein in der Stadt Nippur gefundener Kupferstab ist in 4 Fuß zu je 16 Zoll geteilt. Die Griechen teilten den pus (Fuß) in 4 palaiste (Handbreiten) und 8 daktylos (Finger). In Europa überlebten binäre Aufteilungen von Einheiten bis in die Neuzeit. Hier ei­nige Beispiele.

England:

1 pound = 16 ounces = 256 drams
1 quarter = 8 bushels = 32 pecks = 64 gallons
1 gallon = 4 quarts = 8 pints = 32 gills

Deutschland:

1 Pfund = 16 Unzen = 32 Lot
1 Tonne = 4 Scheffel = 64 Metzen

Schweden:

1 stang = 8 aln = 16 foot

Polen:

1 cwierc = 8 garncy = 32 kwarty = 128 kwaterki

Binär war auch Geld aufgeteilt, z.B., die bis 1837 geltenden alten deutschen "Münz- (Gold- und Silber-) Gewichte: 1 Kölnisch Mark = 6 Unzen = 16 Lot = 64 Quentschen = 256 Pfennig = 512 Heller.

      2.5. Im Altertum wurden 2^k-Zahlen bevorzugt eingesetzt. Der Tierkreis der Babylonier war ursprünglich in 16 Zeichen aufgeteilt, die Griechen nutzten die Periode von 4 Jahren in der Zeitrechnung. Bei den alten Ägyptern ist es die Achtheit der Urgottheiten, bei den Chinesen die mythischen acht Unsterblichen. Acht sumerische Göttinnen helfen beim Erschaffen des Menschen, 16 indische Vidya-Göttinnen stehen Weisen zu Rat, 16 Visionen der Maru Devi sagen die Geburt eines Jina an, der Traum der Königen Maya wird von 64 Brahmanen ausgelegt, ihr Sohn Buddha geht den Achtfachen Weg. Der Grad der Reinkarnation Vishnus wird in Sechzehntel angegeben. Es gibt die 4-, 8-, 16- und 32-Strah­lenembleme alter Kulturen.

      2.6. Die Alten Ägypter wussten, dass jede ganze Zahl als Summe von Zweierpoten­zen darstellbar ist und machten davon Gebrauch, indem sie Multiplikationen und Divisionen durch Addieren von verdoppelten oder halbierten Größen ausführten. Ähnlich wurde noch im Mittelalter Europas gerechnet. Dazu die folgenden Beispiele.

Ähnlich die "russische Bauernmultiplikation" (dritte Spalte), in der man die neben den ungeraden Zahlen links stehenden Zahlen addiert, wobei der beim Halbieren entstehende Rest nicht beachtet wird. Es ist sehr unwahrscheinlich, dass die russischen Bauern dieses Verfahren von den alten Ägyptern übernommen haben. Falls sie es überhaupt übernommen haben, kämen eher die Waräger in Frage. König Karl XII. von Schweden (1697-1718) dachte eine Zeit lang über die Einführung des 64-Zahlensystems. War es der sonderliche Einfall eines Genies oder überdauerte im äußeren Norden Europas eine Tradition des Rechnen mit 2^k-Zahlen länger als anderswo? Denn auch im alten Asien waren binäre Verfahren bekannt. In China diskutierte man im 1. Jt. v.Chr. über die Teilbarkeit von Zahlen der Form 2^k-2. Aus Indien stammt die Legende vom Preis für die Erfindung des Schachspieles mit auf jedem nächsten Felde des Brettes verdoppelter Anzahl von Weizenkörnern. Viele alte Rätsel und mathematische Probleme sind binär konzipiert und dezimal nur mit erheblichem rechnerischem Aufwand zu lösen. Die Ureinwohner Australiens führten im Gedächtnis binäre Aufteilungen durch, denen Europäer nicht folgen konnten.

      2.7. In China gab es die Orakelsprache "I Ging". "Das Tao erzeugt Eines. Aus dem Einem geht Zwei hervor. Drei erzeugt alle Geschöpfe der Welt" heißt es im "Tao te Ging". Das Eine erzeugt Yin und Yang. Yin und Yang ergeben 8 Trigramme, je zwei Trigramme – die 64 Hexagramme des I Ging. Die 8 Trigramme, mit Null für Yin und Eins für Yan gesetzt, ergeben die Zahlenreihe: 001, 010, 011... 111, 000; die 64 Hexagramme - die Zahlenreihe: 000001, 000010, 0000011,... 111110, 111111, 000000. Es ist eine binäre Sprache. Viele alte Sprachen, auch das Indogermanische und Prasemitische, hatten in Opposition zur Mehrzahl eine Zweizahl, den Dual, mit besonderen Pronomen und Deklinations- und Konjugationsformen. Der Linguist J. Vendryes sagt dazu: "Man sollte meinen, dass der Gebrauch des Duals Bedürfnissen entsprach, die verschieden waren von Bedürfnissen, die sich aus unseren heutigen geistigen Gewohnheiten ergeben. Heute sehen wir keinen Grund die Zweiheit der Mehrheit entgegenzustellen." Es ist mehr als ein Bedürfniss der Sprache. Kinder lernen oft die Zahlwörter in der Reihenfolge eins, zwei, vier. "Drei" bereitet zunächst Schwierigkeiten.

      2.8. Binäre Aufteilungen, Maßeinheiten, mathematische Verfahren, sprachliche Re­likte und vieles mehr deuten auf eine von Teilen ausgehende Mathematik und den bi­nären Anfang geistiger Kultur. Das dezimale Zahlensystem setzte sich möglicherweise nur deswegen durch, weil es für den Aufbau einer materiellen Kultur besser geeignet war. Kultur bedeutet Zählen, Haben, mehr Haben. Für den von binären Zusammen­hängen geprägten primitiven Geist ist es belanglos. Die operationellen Nachteile der langwierigen Notation und Schwierigkeiten des Aufbaus von binären Zahlen und Zahlwörtern waren nicht die Ursache der ihm versagten Fortentwicklung, denn sie sind leicht zu überwinden.

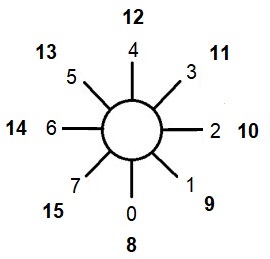
Gesetzt im abgebildeten Oktogramm sind den Radien 2^k-Zahlen zugeordnet für k = 0, 1, 2, 3, 4, 5, 7,... Die Kombinationen der Radien zu 1, 2, 3,... 8 bezeichnen alle ganzen Zahlen von 1 bis 255. Sie werden "Radialzahlen" genannt. Die Zeichen werden direkt vom Zahlensystem abgeleitet, das Zeichen ist ersichtlich Zahl. Substraktive 2^k-Zahlen, eingezeichnet z. B. als Radii unterschiedlicher Farbe, würden die Notation weiter ökonomisieren. Ökonomisch wie die Zahlzeichen wären auch die Zahlwörter. Mit R, (bzw. L), T(bzw. D),. N, M, S, P, H, K entsprechend für 2⁰, 2²,... 2⁷ und vokalisierendem "a" ist z.B. "elf"- MATRA, "zwölf" - MAN, "einunddreißig" - SAMANTRA. Ein Oktogramm mit nach außen und innen gezeichneten Strahlen bezeichnet alle Zahlen von 1 bis 2¹⁶–1 = 65535. Für den untersten Strahl (6-Uhr) 2⁰ gesetzt und entgegen dem Uhrzeigersinn wachsenden k (wie in Zeichnung) erhält man Zahlenzeichen, die "zehn" in babylonischer Notation und "fünf" in einer der griechischen Notationen ähneln.
Binäres Rechnen ist operationell leicht. Man lege Steine auf die Radien und lege Steine hinzu ‑ es ist Addition, man nehme Steine weg ‑ es ist Subtraktion. Zwei Steine auf einem Radius sind ersetzbar durch einen Stein auf dem nächst "höheren" Radius, eine ununterbrochene Reihe von Steinen – durch einen Stein auf dem nächst höheren und einen subtraktiven Stein auf dem "niedrigsten" Radius. Soviel die Regeln des Spieles.

Für Multiplikation würde sich ein Spielbrett eignen, z.B. ein Schachbrett.

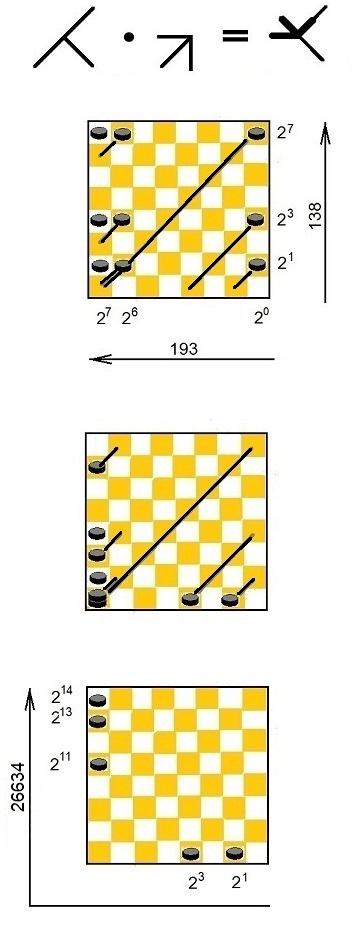
Das Spiel sei wieder 138 mal 193. Das rechte untere Feld hat den Wert 1, die nacheinander folgenden horizontalen und vertikalen Felder - die Werte 2, 4, 8,... Die Steine werden mit Läuferbewegung auf die untere und linke äußerste Feldreihe verschoben und entsprechend den Regeln geordnet. Mit einem aus drei Steinen aufgebauten Turm im linken oberen Feld, sind Produkte bis 2¹⁶-1 zu errechnen. Auch dieses Spiel lässt sich auf vielerlei Art spielen, z. B. auf Pflanzenfaser- oder Bastplättchen mit eingezeichneten Bildern für Zweierpotenzen. Es könnten Spielkarten, z.B. Skatkarten sein. Zwei Spiele (2mal 32 Karten) sind nötig. Buben werden als 2¹⁴ und 2^l5 gespielt, die roten Farben (Kreuz und Herz) sind subtraktiv. Es ist einfaches Kartenlegen. Spielkarten aus Papier waren in China ursprünglich Geld so ähnlich, dass nicht zu erkennen ist, ob Geld Spielkarten voranging oder umgekehrt. Man konnte mit Geld um Geld gespielt haben.

Division, das umgekehrte Spiel, ist Spiel im eigentlichen Sinne, gute Spieler spielen es schnell und fehlerfrei, doch es geht auch routinemäßig, wie an anderer Stelle gezeigt wird. Für größere Zahlen als 255 nimmt man größere Spielbretter z.B. Halma mit 16 mal 16 = 256 Feldern oder größere Kartenspiele, z.B. Bridge mit 4 mal 13 = 52 Karten. Auch Radialzeichen für größere Zahlen sind leicht zu konstruieren. Man kann vom Kreis ausgehen und nach innen wie nach außen Radien und fette Halbradien ziehen, womit man auf 2³²-1 kommt. Noch vor nicht langer Zeit wäre so jeder Bewohner des Planeten zu identifizieren und er könnte selbst das Zeichen ästhetisch ausgestalten mit einer zweiten Farbe für subtraktive Größen. In der Vergangenheit waren solche Zahlen praktisch nutzlos, da viel zu groß, doch im Spiel würden sie vorkommen, etwa auf einem schachbrettartigen Spielplatz oder auf einem Spielplatz mit konzentrisch in das Oktogramm gezeichneten Kreisen. Man kann das Spiel natürlich auch in die Länge ziehen, z.B., indem man eine Reihe von Kästchen in den Sand ritzt.

Dieses Zahlensystem ist kein Stellenwertsystem, denn Zahlen werden durch eine Summe von Stufenzahlen, die ihre besonderen Zeichen haben, dargestellt, wogegen im Stellenwertsystem die Stufenzahlen durch Ziffern, d.i. durch die Zeichen der Basiszahlen dargestellt werden. Es fehlt der Begriff "Null", mit dem der menschliche Geist in der Vergangenheit enorme Schwierigkeiten hatte. Es ist ein Dualsystem, das in ein beliebiges 2^k-Stellenwertsystem aufgegliedert werden kann, doch in das Dualsystem sofort rückführbar ist. Die Folge ...8, 4, 3, 2, 1, 1/2, 1/4, 1/8... läuft ununterbrochen von Eins auf immer größere und immer kleinere Größen zu. "Eins" ist sein Mittelpunkt, für Null kein Platz.

      2.9. An dieser Stelle, ein Zitat aus der Arbeit von W. von Soden⁷ als Zwischenstück, das weitere Ausführungen erheblich erleichtert: "Zusammenhängend konnten die Sumerer ihre Gedanken nicht darstellen, weder in den Bereichen der Natur, der hergestellten Gegenstände und der Theologie noch in denen der Mathematik..."(S.139). "Damit war man zu einer rein positionellen Zahlenschreibung gekommen wie viel später im Rahmen des Dezimalsystems Inder, Araber und wir. Da man aber ein unserem Komma entspre­chendes Zeichen nicht verwendete, war bei mehrstelligen Zahlen der Stellenwert normalerweise nicht ersichtlich. Eine Sexagesimalzahl wie 58 45 40 entsprach also dezimal nicht nur 208800+2700+40=211540, sondern auch dem Sechzigfachen usw. und einem Sechzigstel usw. davon, sofern der Zahl nicht eine Benennung folgte, die sie eindeutig machte. Die Babylonier haben es verstanden, hier aus Not eine Tugend zu machen und mit den Zahlen ohne eindeutigen Stellenwert ganz raffiniert zu rechnen, weil ihnen bei den Zwischenzahlen einer längeren Rechnung der Stellenwert gleichgültig sein konnte..."(S.158-159). "Für das Rechnen bestand im Alten Orient die Schwierigkeit, dass man zwar Additionen und Subtraktionen auch bei sehr großen Zahlen durchführen konnte, nicht aber Multiplikationen und Divisionen. Das zwang zur Anlage von Multiplikationstabellen und, weil man Divisionen nur als Multiplikationen mit dem Reziproken des Divisors konzipieren konnte, auch von Reziprokentabellen schon durch die Sumerer. Dazu kamen Tabellen von Potenzen und Wurzeln. Spätesten in der altbabylonischen Zeit schuf man zu den für das Rechnen notwendigen Tabellen andere hinzu, die auf ein theoretisches Interesse an den Eigentümlichkeiten des Zahlenreiches schließen lassen. So verfolgte man die sexagesimal als 3 45 erscheinende 225 bis zur zehn­ten Potenz, weil es bei dieser Zahl ungewöhnlich gleichartige Zahlenfolgen gibt. Die Potenzzahlen für die 2 führte ein Gelehrter bis zur 2³⁰ durch und bildete dann zu der bei uns zehnstelligen Zahl noch die Reziproke, sexagesimal eine noch längere Zahlenfolge. Irgendein praktisches Interesse konnten solche Tabellen nicht haben; wir hören aber nichts darüber, warum man so ungewöhnliche Tabellen anlegte" (S.159). "Wie ist es möglich, dass eine Mathematik, die leistungsfähiger war als die griechische in ihren Anfängen, ohne jede Formulierung der Erkenntnisse auskam, von denen wir so vielfältig Gebrauch machen? Man kommt schwer an der Annahme vorbei, dass es in Babylonien im Gegensatz zu dem, was fast überall als gesicherte Erkenntnis gilt, auch ein sprachfreies Denken gab, das ganz ohne formulierte Erkenntnisse sehr effizient arbeiten, dabei aber gewisse Grenzen nie überspringen konnte. Was diese Grenzen historisch bedeuten zeigt höchst eindrucksvoll die Tatsache, dass die babylonische Mathematik nach dem großartigen Aufschwung der altbabylonischen Zeit an die 1000 Jahre stehen blieb, ja wahrscheinlich sogar an Leistungsfähigkeit stark verlor" (S.161).

      2.10. Der Gang bis hierher war nötig, um einen Tausch vorzuschlagen. Das Magische, Heilige, Kultische, Rätselhafte, Zauberische, Widersinnige der alten Mathematik - das alles - für eine Annahme. Für so wenig? Wie man es nimmt.

Nehmen wir an ein isoliertes primitives Volk ist bei der binären Mathematik geblieben und hat sie im Spiel fortentwickelt. Es ist Mathematik der Exponenten, das Weber-Fechnersche Gesetz kommt zur Wirkung, sie hören und fühlen die mathematischen Zusammenhänge, können Mathematik spielen, rechnen brauchen sie nicht. Der pleistozäne Umbruch, mit dem unsere Nacheiszeit begann, zwingt Gruppen dieses Volkes aus der Isolation heraus zum Zusammenleben mit Gemeinschaften von Kulturmenschen, die im Dezimalsystem, bzw. im Fünfer- oder Zwanzigersystem, rechnen. Gruppe und Gemeinschaft müssen kommunizieren, auch mathematisch kommunizieren. Die binäre Mathematik ist nicht vermittelbar, dezimales Rechnen scheint den Primitiven widersinnig. Die Gruppe ist zahlenmäßig und kulturell unterlegen, doch merkt, dass die binäre Mathematik für die Aufgaben materieller Kultur einsetzbar ist, ohne von der mit rigiden Verfahren arbeitenden Gemeinschaft als Rechnen erkannt zu werden. Allerdings nur dann, wenn es gelänge Zahlen des Dezimalsystems ins binäre System und umgekehrt unmerklich und schnell zu übersetzen. Es ist das Problem des Kartenlegers, der nur dann zaubern oder wahrsagen kann, wenn er die Um­rechnung schnell im Gedächtnis durchführt.

      2.11. Die Umrechnungsverfahren von Dezimalzahlen in Dualzahlen und umgekehrt sind allgemein bekannt. Bei Zahlen über Tausend werden sie umständlich. Leichter geht es mittels der Zahl 15=16-1, binär (10001)₂, die sich von der binär "runden" Zahl 2⁴ nur um 1 unterscheidet und deren binäre Vielfache schon bei 30 ins Dezimalsystem laufen. Bei binären Multiplikationen einer Zahl mit 15 wird von der um vier Nullen verlängerten Zahl, die Zahl subtrahiert. Im Folgenden werden binäre Zahlen mit Steinen auf Tafeln gespielt. Subtraktive Steine werden farbig angezeigt, die Exponenten über 2 von rechts nach links gezählt. Beispiel: 27·15=405

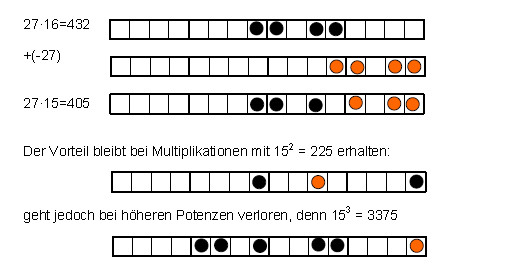
Es war also günstig 2^k-Vielfache von 15 einzusetzen, denn ohne das Spiel wesentlich zu verändern, sind mit der Basis 60 bzw. 120 und den weiterhin günstigen Stufenzahlen 3600 bzw. 14400 entsprechend höhere Zahlen zu erreichen. Die Zählbasis 60 ist die der Sumerer, eine Zählbasis 120 wurde in Europa genutzt. Binär unterscheiden sie sich um eine Null.

Zahlen wurden bei den Sumerern mit 1 bis 9 Einern und 1 bis 5 Zehnern angegeben. Die höheren Stufenzahlen waren an ihrer Position innerhalb des Zahlzeichens erkennbar, bei fehlender Stufenzahl war der Abstand zwischen den Stufenzahlen größer. Für die dezimal rechnende Gemeinschaft war Zählen bis 60 und die Angabe von Mengen zu 60 keine erhebliche Belastung, zumal die Zahlennotation es denkbar leicht machte.

Diese Art der Notation ermöglicht zudem die Anwendung eines Verfahren zur Übersetzung von sexagesimalen Zahlen in Dualzahlen, das schneller zum Ergebnis führen kann. Dabei wird aus der sexagesimalen Zahl die größtmögliche 2^k-Zahl herausgenommen und der Vorgang so viele Mal wie nötig wiederholt. Im 60er-System sind diese Zahlen leicht zu merken, denn es ist

1·60 + 4 = 2⁶
4·60 + 16 = 2⁸
8·60 + 32 = 2⁹
(16 + 1)60 + 4 = 2¹⁰
(32 + 2)60 + 8 = 2¹¹
1·60² + 8·60 + 16 = 2¹²
2·60² + 16·60 + 32 = 2¹³
4·60² + (32 + 1)60 + 4 = 2¹⁴
(8 + 1)60² + 6·60 + 8 = 2¹⁵, usw.

Zahlen bis zu 60 werden direkt übersetzt, wobei man die bequemen Konfigurationen des Dutzend (1100)₂ und der Mandel (1111)₂=(10001)₂ zur Hilfe nehmen kann. Die arithmetischen Operationen sind dann auf einem Spielbrett leicht durchzuführen. Das Ergebnis wird im umge­kehrten Verfahren in eine sexagesimale Zahl übersetzt.

In Europa wurde neben Zehn und Hundert mit Dutzend (12), Mandel (15), Schock (60), Großhundert (120) und Gross (144), (binär 10010000), gerechnet, die alle gute Umrechnungszahlen sind. Auch der hier auftretende Begriff der "Großen Mandel" gleich 16, ist nur in diesem Zusammenhang erklärbar. Erklärbar auch der Name des neunten Zahlwortes, das in vielen Sprachen (auch in Mittelamerika) von "neu" abgeleitet wird, und der Bruch der Zahlwortreihe bei seize - dix-sept im Französischen.

Für das Rechnen mit der Zahl 15 und ihren binären Vielfachen eignet sich das 4m Spielbrett mit der Anordnung der Exponenten über 2, wie in der abgebildeten Tafel. Diese Anordnung entspricht dem 16-er Stellenwertsystem.

Sie ergibt folgende günstige Konfigurationen für 60 und deren Vielfache: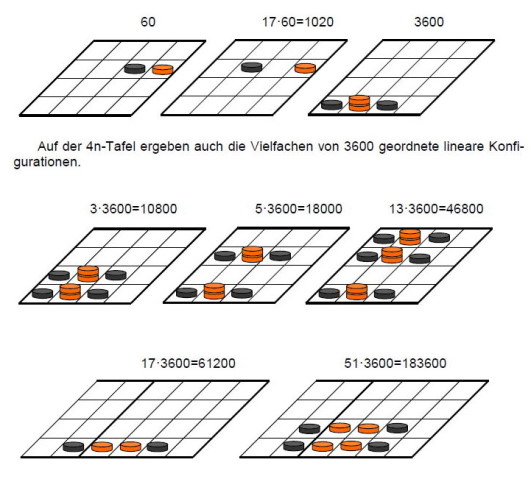

      2.12. Die Alten Ägypter rechneten in einem nicht positionellen dezimalen Zahlensystem mit besonderen Zeichen für die Stufenzahlen (Einer, Zehner, Hunderter usw.), die bis 9-mal wiederholt wurden. Zehn Zeichen derselben Art werden durch das nächst höhere ersetzt. Die Notation ist langwierig, das Rechnen umständlich. Doch die Notation ist günstig bei Umrechnungen ins Dualsystem und umgekehrt. Man kann nämlich ein Zeichen durch zehn nächstniedrigere Zeichen ersetzen und dem niedrigeren Zeichen zufügen, was das zuvor beschriebene Herausnehmen und Hinzufügen der 2^k-Zahlen erleichtert, folglich einfacher ist als die Umrechnung von Vielfachen von Zehnerpotenzen. Hat man einmal die Zahl übersetzt, wird die arithmetische Operation, wie gezeigt, auf dem Spielbrett ausgeführt. Auch Teilen ist routinemäßig möglich. Dazu als Beispiel die schon angeführte Teilung von 26634:138=193. Der Stein auf dem rechten Rande des Bretts steht wieder für 2⁰.

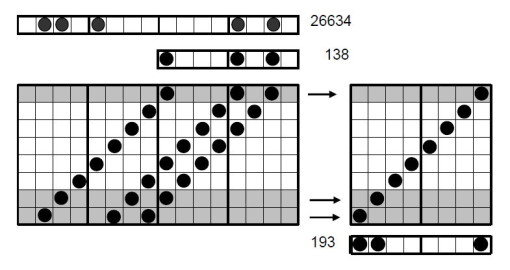
Auf der linken Tafel sind die Reihen zu suchen (markiert), die zusammengefügt die Zahl 26634 ergeben, auf der rechten Tafel werden die entsprechenden Reihen zusammengefügt. Für Multiplikation ist das Verfahren dasselbe, nur die Pfeile entgegengesetzt. So gesehen ist die ägyptische und alte europäische Rechenart eine dezimale Analogie des dualen Verfahrens.

Division durch Multiplikation mit dem Reziprokwert des Divisors ist die andere Möglichkeit. Der duale Reziprokwert ist leicht zu finden. Es wird auf beliebiger Tafel mit Steinen gespielt. Mit „o“ sind leere Felder bezeichnet. In binärer Darstellung ist der schwarze Stein eine Eins, der weiße Stein eine Null. Es ist dann 3=(11)₂, 5=(101)₂, 7=(111)₂, usw.

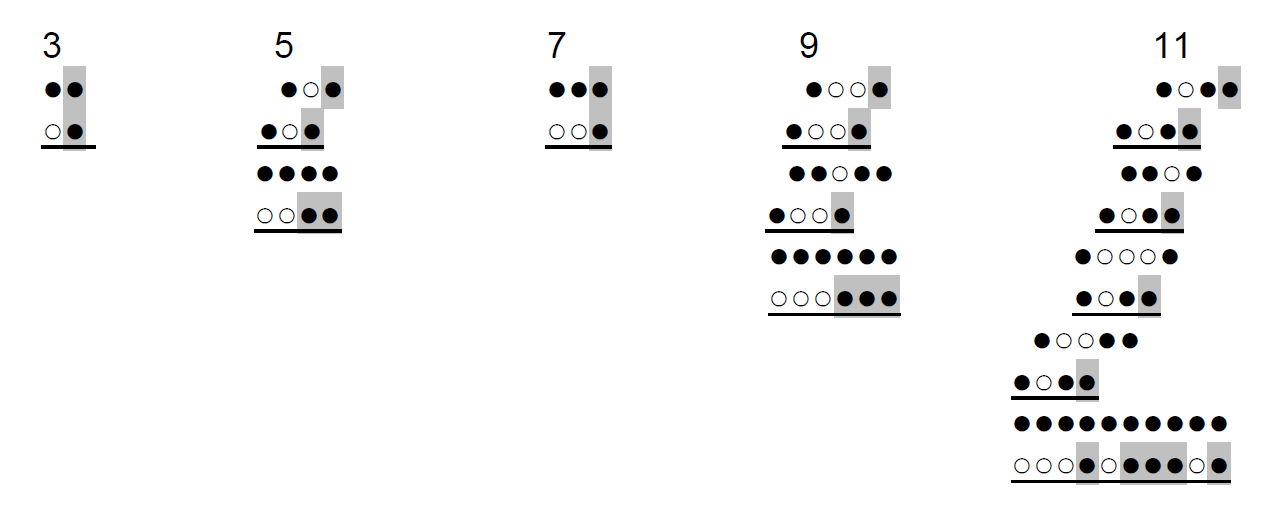
Bei langen Perioden wird man für praktische Berechnungen die geforderte Genauig­keit festsetzen oder die Kehrzahl als Summe der Kehrzahlen mit den regelmäßigen Sätzen 2/3, 4/5, 4/7, 8/9, 8/15, 16/17, 16/31, 32/33, usf. oder bequemer nur mit 2/3, 4/7, 8/15, 16/31, 32/63 usf. berechnen, wobei mit drei Gliedern die Differenz vom exakten Wert meist erst an fünfter Dezimalstelle erscheint, z.B. 16/29 = 0,551724, im Vergleich zu 16/29≈8/15 + 2^-3×1/7 + 2^-7×1/15 = 0,551711.

Die von den Ägyptern tabellarisch zusammengestellten Summen von Stammbrüchen gehen von verdoppelten Kehrzahlen aus.

2/5 = 1/3 + 1/15;     2/7 = 1/4 + 1/28;     2/9 = 1/5 + 1/45;

2/11 = 1/6 + 1/66;     2/13 = 1/7 + 1/91;     2/15 = 1/8 + 1/120;     2/17 = 1/9 + 1/153; usf.

Die Regel der Aufteilung vieler zweigliedriger Summen von Stammbrüchen ist leicht erkennbar, da die um eins vergrößerten Nenner der Kehrzahl zu halbieren sind, und die Nenner des zweiten Gliedes sich als Produkt des Nenners der Kehrzahl und des Nenners des ersten Gliedes errechnen:

2/5 = 1/3 + 1/15;     (5+1)/2 = 3       5x3 = 15
2/11 = 1/6 + 1/66;   (11+1)/2 = 6     11x6 = 66

Ableitbar sind jedoch auch komplexe Aufteilungen wie die zuvor angeführte von 28/97 zu 1/4+1/56+1/97+1/194+1/388+1/679+1/776:

28/97 = 14(2/97) = 14(1/49 + 1/49×97) = 2/7 + 2/7×97 = 1/4 + 1/4×7 + 2/7×97 =
= 1/4 + 1/56 + 1/56 + 2/7×97 = 1/4 + 1/56 + [7(8+4+2+1) + 8]/7×8×97=
= 1/4+1/56+1/97+1/194+1/388+1/679+1/776

In dieser Auflösung verbirgt sich die Folge der 2^k-Zahlen 1, 2, 4, 8.

Eine andere komplexe Aufteilung, nämlich die Angleichung von 2/89 zu 1/90+1/92+1/4094+1/8010+1/8188 ist merkwürdig. Es ist als wollte man an 1/2¹²= 1/4096 und 1/2¹³= 1/8192 herankommen.

Die binäre Kehrzahl ist eine Summe von 2^-k-Zahlen. Diese Zahlen sind Glieder einer Dualentwicklung und zugleich Stammbrüche. Das erste Glied enthält den Hauptteil des Bruches, die Anzahl der in Rechnung genommenen Glieder entspricht der geforderten Genauigkeit. So gesehen ist die altägyptische Bruchrechnung eine Analogie des binären Verfahrens die den Vorteil des dezimalen Systems nutzt, dass jeder echte Bruch mit ganzzahligem Zähler und Nenner in eine endliche Summe von verschiedenen Stammbrüchen zerlegbar ist. Doch im Gegensatz zur Summe binärer Stammbrüche, die als Dualentwicklungen direkt addierbar und wie ganze Zahlen multiplizierbar sind, ist es in dezimaler Notation nicht möglich. Die genaue Darstellung von Brüchen mag die Ägypter fasziniert haben, doch die Zerlegungen zeigen die Größe der Kehrzahl undeutlich und sind in Anwendungen unpraktisch. Es macht die ägyptische Bruchrechnung widersinnig.

Der Autor (Achmes) des Papyrus Rhind beginnt sein Werk mit folgender Einführung: "Genaues Rechnen. Einführung in die Kenntnis aller existierenden Gegenstände und aller dunklen Geheimnisse." Aller dunklen Geheimnisse? Eine alte Bezeichnungsweise für Brüche, die bei der Bemessung von Getreidemengen verwendet wurde hatte Zeichen für 1/2, 1/4, 1/8, 1/64 ⁽⁹⁾. Diese Zeichen sind Teile des Auges des Falkengottes Horus, das von Seth in Stücke gerissen wurde. Die mythische Herkunft dieser Zeichen, weist auf seine besondere Bedeutung. Der Mythos sagt, dass die Götter die Vorgänge der Welt als Halbierungen und Verdoppelungen sahen - und dass es nicht mehr so ist.

      2.13. Die von v.Soden angeführten Potenzen der Zahl 225 ergeben sexagesimal, (in dezimaler Notation und Bezeichnung der Position durch ein Komma), folgende Reihen von Zahlen:

225                                (3, 45)₆₀
225²                         (14, 3, 45)₆₀
225³                   (52, 44, 3, 45)₆₀
225⁴          (3, 17, 45, 14, 3, 45)₆₀
225⁵  (12, 21, 34, 37, 44, 3, 45)₆₀, usw.

Die gleichartigen Zahlenfolgen sind nur so ungewöhnlich, wie etwa die von (10/2·10/2)^k mit den Zahlen 25, 625, 15625, 390625, 9765625, 244140625, usw.

Es ist jedoch:
2⁴·225 = 60²
2⁸·225² = 60⁴
2¹²·225³ = 60⁶
2¹⁶·225⁴ = 60⁸
2²⁰·225⁵ = 60¹⁰, usw.

Das ungewöhnliche theoretische Interesse der Alten Babyloniern - "spätestens in der altbabylonischen Zeit" - sowohl für sehr hohe Zweierpotenzen, wie für Potenzen der Zahl 15, die binär die eigentliche Basis des 60er Systems ist, (225=15²) zeigt eine weitere Möglichkeit zur Umrechnung von Sexagesimalzahlen in Dualzahlen und umgekehrt.

Die Vernachlässigung des Stellenwertes in Berechnungen mit sexagesimalen Zahlen entspricht der binären Rechenweise, wo es nicht auf den Stellenwert, sondern auf die Konfiguration der Zweierpotenzen ankommt. Es ist gleichgültig, ob man z.B. mit 832 oder 13 oder 13/2048 rechnet, also mit (1101000000)₂ oder mit (1101)₂ oder mit (0,00000001101)₂, denn man wird es mit der Konfiguration für 13 auf dem passenden Spielbrett tun. Am Ende der Berechnung werden dann die Nullen hinzugefügt oder weggenommen, ähnlich wie im Rechnen mit Dezimalzahlen.

      2.14. Für dezimal (bzw. vigesimal)-binäre Umrechnungen eignen sich die Zahlen:

(1) (2⁴-1)2^k, mit den Zahlen 15, 30, 60, 120,...

(2) (2⁶+1)2^k, mit den Zahlen 65, 130, 260, 520,...

(3) (2⁸-1)2^k, mit den Zahlen 255, 510, 1020, 2040,...

Ein Zahlensystem mit der Basis 260 entspricht dem im mesoamerikanischen Kulturkreis genutzten Heiligen Jahr. Wie das 60er System der Babylonier, ist es ein Umrechnungssystem. Die Zyklen der Zeitrechnung der Maya auf einem dreireihigen Senet-Brett gespielt, wie es im Grabe des ägyptischen Königs Tut-Anch-Amun gefunden wurde, doch viel älter ist (es könnte sehr wohl ein Senet-Brett gewesen sein, auf dem der Gott der Weisheit Toth im Spiel mit dem Mondgott Chons die fünf letzten Tage des Jahres für die Himmelsgöttin Nut gewann, derselben, die vom Sonnengott Re, wegen einer Liebesaffäre mit dem Erdgott Geb, an keinem Tage des Jahres gebären zu können verflucht wurde), ergeben bei der angezeigten Anordnung der Exponenten über 2 (die Spalten entsprechen dem achter Stellensystem) die folgenden Konfigurationen von Steinen (auf Potenzstelle 2⁸ der Kalenderrunde und 2⁹ der doppelten Kalenderrunde sind es zwei Steine):

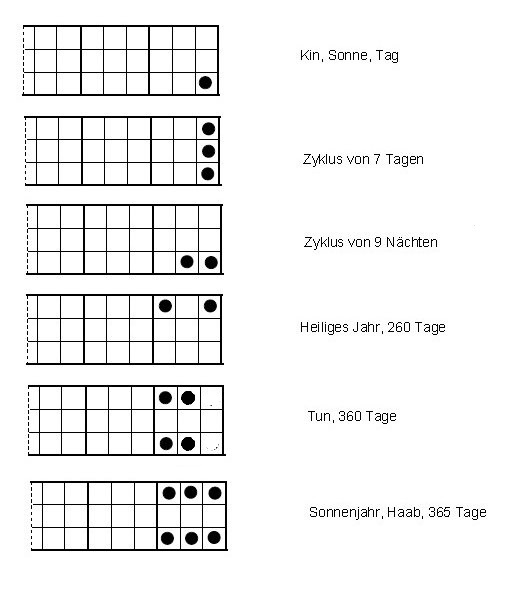
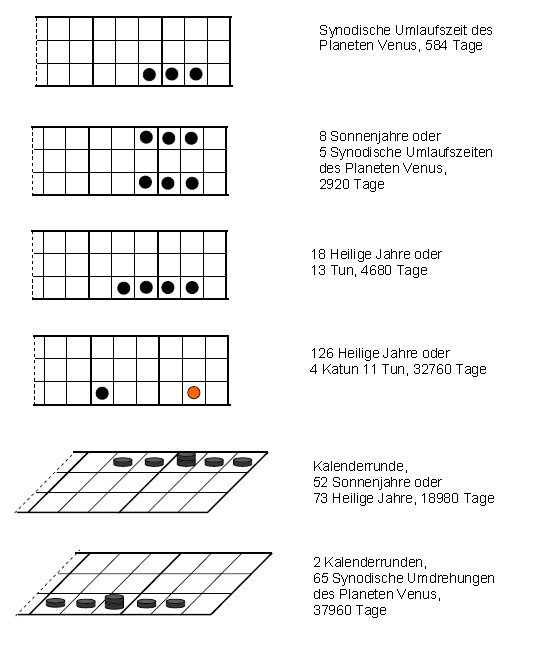
Das Rechnen mit 260 ist ähnlich wie mit 60. Bei Multiplikation einer Zahl mit 260, wird der um acht Nullen verlängerten Zahl die um zwei Nullen verlängerte Zahl hinzugefügt.

Beispiel: 73×260 = 18980.
100100100000000
000000100100100
100101000100100

In längeren Zeitabschnitten rechneten die Maya mit dem Katun von 7200 = 225×2⁵ Tagen. Es ist die verdoppelte dritte Stufe des 60er Systems der Sumerer. Die Übersetzung einer beliebigen Zahl angegeben in Perioden der Zeitrechnung der Maya in eine Zahl des 2^k-Zahlensystems ist mittels der angeführten Konfigurationen von Steinen spielerisch leicht. Ausgedrückt im Achtersystem und Tagen beträgt die doppelte Kalenderrunde (112110)₈, 18 Heilige Jahre oder 13 Tun (11110)₈, die synodische Umdrehung des Planeten Venus (1110)₈, das doppelte Heilige Jahr (1010)₈, 126 Heilige Jahre oder 91 Tun (100010₎₈. Die letzte Konfiguration ist auch für sehr große Zahlen geeignet, da auf 3m-, 4m- und 6m-Brettern spielbar.

      2.15. Im Teil "Die präkolumbische Tradition" schreibt A. Castiglioni⁸: "Im alten Mexiko galt das Sonnenjahr, das in Zeitabschnitte von dreizehn und zwanzig Tagen untergeteilt war. Das System wird außerordentlich kompliziert, wenn man bedenkt, dass zusätzlich während des ganzen Jahres die jeweiligen Zeitabschnitte von fünfundsechzig und drei Tagen einem übernatürlichen, mit besonderen Funktionen ausgestatteten Wesen unterstanden ..."
Diese Ergänzung des Heiligen Jahres, einer Abwertung und Profannation nahe, hat einen mathematischen Grund: es ist die Zahl 68, binär (1000100)₂, das Vierfache von 17, (10001)₂. Dort wurde auch mit 17 gerechnet. Spieltechnisch ist 17 günstiger als 15

17 = (10001)₂
17² = 289 = (100100001)₂
17³ = 4913 = (1001100110001)₂

15 = (10001)₂
15² = 225 = (100100001)₂
15³ = 3375 = (110100110001)₂

da auch 17³ in der Konfiguration (10001₃0001₃0001)₂ mit dreifachen Steinen (1₃) auf Potenzstelle 2⁴ und 2⁸ leicht spielbar ist, doch hat den Nachteil, dass 2^k-Vielfache von 17 keine Vielfachen von 20 ergeben. Da jedoch im mesoamerikanischen Raum auch mit 15 gerechnet wurde, lag nahe die Vorteile der Zahlen 15 und 17 in der Zahl 15×17=255=(100000001)₂ zu verbinden. Sie ist für Rechnen mit großen Zahlen vorteilhafter als 260 durch die Nähe zu 2⁸ und läuft bei 1020 ins Zwanzigersystem. Von der binären Basis des Katuns 225 unterscheidet sie sich um die binär günstige Zahl 30=(100010)₂, was sich auf dem 4m-Spielbrett in den Konfigurationen des Katuns und der Zahl 2⁵×255 und zeigt:

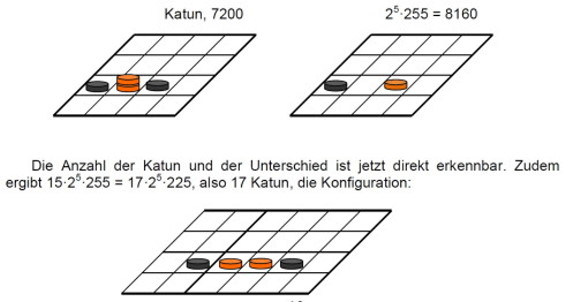
      2.16. Die Koinzidenz des Vielfachen der Zahl 73 mit dem Jahr und der synodischen Um­laufszeit des Planeten Venus ist diesen Betrachtungen zufolge rein mathematisch. Ein physikalischer Zusammenhang ist ebenso wenig ersichtlich wie etwa der Zusammenhang zwischen der Fußlänge eines zweibeinigen Wesens und Gravitation. Dennoch, mit einem "mittleren Fuß" gerechnet (der englische Fuß gleicht 0,3048 m, der altägyptische 0,3079 m), schreibt man für h=gt²/2 nur h=16t², mit einem "mittleren" altschwedischen Stang einfach h=t². Das jedoch kann nur Zufall sein, da die Alten zwar den Tag in Sekunden teilten, diese aber so genau nicht messen konnten. Es gibt allerdings neben der herkömmlichen Sekunde, noch eine artspezifische Sekunde, nämlich den Zeitintervall, in dem 16 gleichmäßig nacheinander folgende Schwingungen derselben Art als Ton hörbar sind. Direkt folgt daraus nichts, und zwar deswegen nicht, weil auf die Einfälle eines Spielers aus den Regeln des Spieles nicht zu folgern ist.

      2.17. Wenn der Mythendichter nach der Erschaffung der Welt, Gott am siebenten Tag ruhen lässt und später von der Steinigung eines am Sabbat Holz sammelnden Mannes berichtet (4 Mose 32ff.), dann sagt er, dass diese Periode wichtig ist. Nachdem was hier gesagt wurde ist sie mathematisch wichtig. Die Zeitkorrekturregel einer binären Kultur würde lauten: Zähle die Tage bis sieben, nach 13×(2²×7)=364 Tagen warte einen Tag bevor du von Anfang beginnst, doch nach vier solchen Perioden zwei Tage, außer der 2⁷-ten Periode, nach der du nur einen Tag wartest. In dieser Zeit sind 128x364+128+31=46751 Tage verstrichen, woraus sich ein mittleres Jahr von 46751/128=365,2421875 Tagen errechnet, das vom tropischen Jahr um den Bruchteil einer Sekunde abweicht. Die Macht derer, die zu "Allwissenden" der Kulturvölker wurden, beruhte auf einem zahlreichen Mittelstand irreführend eingeweihter Adepten – den Priestern. Die Beobachtung der Umlaufszeit des Mondes oder des Planeten Venus oder des heliakalen Aufganges eines Sternes ist schwierig und ungenau, da die Zyklen naturgemäß fluktuieren. Die Adepten mögen beobachtet und gerechnet haben, wie viel sie wollten, sie ermittelten die Länge des wahren Jahres immer falsch und wurden von Männern, die nicht weiter als auf ihren Nabel schauten, zurechtgewiesen. Worauf rechneten diese Optimisten falls es schief ginge? In der Spätzeit der Maya, als klar wurde, dass es schief geht, begann man nur bis 13 Katun zu rechnen. 13 Katun (93600 Tage) sind fast genau um 98 Tage länger als 2⁸ Tropische Jahre (93502,0032 Tage). Am Ende gaben sie ein Zeichen. Es lief überall schief. In Europa nicht so schief, doch auch hier räumte die französische Revolution mit Autokratie, Theokratie, Aristokratie, mit binären Maßeinheiten und nicht dezimalem Zählen auf. Die Säuberungsarbeiten sind im Gange. Würde Karl XII. das 64er-Zahlensystem eingeführt haben, wäre vermutlich maschinelles Rechnen früher in der Welt, Genetik hätte andere Gestalt. Mathematik ist Macht, sie verändert die Welt, ob man will oder nicht. Die Alten wollten es nicht. Daran gingen sie unter. Damit auch. Zum Bedenken für Optimisten, die auf Teufel komm raus in technisierte binäre Systeme investieren.
Soviel das Tauschgeschäft. Manchmal merkt man erst sehr spät was man sich eingehandelt hat.

Reflexion nach vielen Jahren
     Könnte es wirklich so gewesen sein? Man wird es nie erfahren. Also würde ich heute auf jegliche gesellschafts-politische Hypothesen verzichten und schlicht fragen: Kann man die von der Wissenschaft festgestellten Zusammenhänge bei anderen Grundannahmen bündiger beschreiben? Dann gäbe es einerseits Tausende Seiten zum magischen Denken in den Anfängen der Mathematik und noch einmal Tausende Seiten zu den Sonderlichkeiten der altertümlichen Arithmetik, anderseits eine kurze Abhandlung, deren logischen Zusammenhang man irgendwann aufgreifen könnte. Und damit sind wir wieder bei Magie. Denn diese Grundannahmen sind nicht zu erdenken.

Die Wende?
Könnte es wirklich so gewesen sein? Jahre nach Veröffentlichung dieser Fassung fand ich bei "Wilhelmy, Herbert, Welt und Umwelt der Maya, R. Piper & Co Verlag, München, Zürich, 1981", Seite 35, folgende Aussage:
"Sie (die Chilam-Balam Bücher) enthalten Prophezeiungen, Rituale und in Mythen gekleidete Chroniken historischer Begebenheiten in der alten Zeitrechnung. Bereits erfolgte geschichtliche Abläufe sind in Form von Weissagungen gekleidet, so dass diese, da die Maya an eine zyklische Wiederkehr der Ereignisse in Abstanden von 256 Jahren glaubten, den Priestern eine göttliche Offenbarung für die Zukunft bedeuteten."

Mit meiner Abhandlung wäre ein der Zeitrechnung der Maya zugrundeliegender Zyklus von 256 Jahren begründet, und die Vermutung binären Rechnens in anderen Erdteilen nicht mehr so ganz phantastisch.


Literatur

1. Thompson J. E. S. Maya Astronomy, "Phil. Trans. R. Soc. Lond.", A 276, 83-94 (1974).
2. Spinden H. J., Maya Art and Civilization, Indian Hills, Colorado, 1957.
3. Wussing H., Mathematik in der Antike, Leipzig, 1965.
4. Bourbaki N., Eléments d´histoire des mathématiques, Paris, 1960.
5. Volodarski A. I., Matematika v drevnei Indii. Istoriko-Matematitcheskie Issledovannia,
   XX Moskva, 1975, pp. 282-298.
6. Schlenther U., Die geistige Welt der Maya, Berlin, 1965.
7. von Soden W., Einführung in die Altorientalistik, Wissenschaftliche Buchgesellschaft, Darmstadt, 1985.
8. Castiglioni A., Weltgeschichte der Magie, Arthur Moewig Verlag, Rastatt, 1988.
9. Simonyi K., Kulturgeschichte der Physik, Verlag Harri Deutsch, Thun Frankfurt am Main, (1990).
10. Lehman J., So rechneten Ägypter und Babylonier, Urania Verlag, Leipzig, Jena, Berlin, (1994).

---

---